Первые попытки описания экономических процессов языком математики были сделаны к середине XIX века. Вначале французский профессор А.Курно опубликовал в 1838 г. книгу «Исследование математических принципов теории богатства», а позднее, в 1853 г. немецкий экономист Г.Госсен издал книгу «Развитие законов общественного обмена и вытекающих отсюда правил общественной торговли». Однако труды пионеров экономико-математического направления не вызвали интереса ни в научных кругах, ни в массе всех иных читателей: книги почти не продавались.
Курно пробовал переиздавать свой труд под разными названиями, изымая из него математические символы и формулы – все безрезультатно. А для Г.Госсена равнодушие к его труду было таким ударом, что незадолго до своей смерти в 1858 году он выкупил и уничтожил практически весь тираж книги. И лишь спустя треть века книга Госсена была обнаружена профессором Адамсоном и переиздана в 1889 году. Лишь тогда идеи пионеров нового направления были восприняты научной мыслью.
К началу ХХ столетия экономико-математическая школа уже окончательно сформировалась. Причем термин «школа» не следует понимать таким образом, что у представителей этого направления имелась общая программа – их объединял лишь метод исследования экономических явлений.
Что же касается вопроса о формировании управленческой математической школы, то здесь имеются свои нюансы. Долгое время научное сообщество вообще не разделяло экономические и управленческие вопросы; казалось, производственная деятельность настолько тесно связывает проблемы управленческого и хозяйственного плана, что провести между ними четкий водораздел не представляется возможным. Подобно тому, как Адам Смит не разделял функции собственника бизнеса и предпринимателя (они представляли для него монолитное и неделимое единство), так и экономисты первой половины ХХ века считали управленческие вопросы частью экономической науки.
Формализация хозяйственных задач, составление уравнений спроса и предложения, описание равновесной рыночной экономики, сделанные Л.Вальрасом, В.Парето, А.Маршаллом и другими учеными придало сильный импульс к исследованию задач управления производством и созданию не только теоретических, но и практических моделей макро и микроуровня.
Мы уже упоминали выше, что образование первого в мире социалистического государства – СССР в 1922 году послужило качественным толчком к созданию целого ряда работающих хозяйственных и управленческих моделей, основанных на математическом методе.
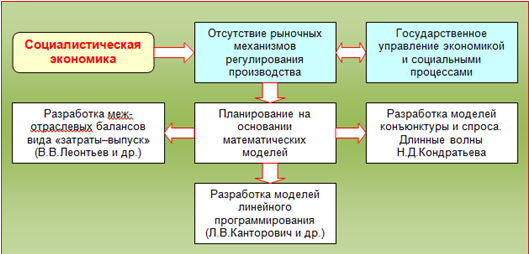
В определенной мере математический подход должен был стать не только вспомогательным инструментом перевода экономики на научные рельсы, – он должен был в известной степени заменить рынок и рыночное управление хозяйственной системой (см. рис.1).
Экономика без эксплуатации человека человеком, без инфляции и безработицы, с централизованным планированием как несущим элементом – таковой в идеале мыслилась социально-экономическая структура общества – более справедливого, без денег и рынка.[1]
Решить эту грандиозную по масштабам задачу изменения системы управления экономикой было необычайно сложно, тем более, что раньше этого еще никто не делал. Попытки отмены денег и установления прямых распределительных отношений путем продразверстки и введения военного коммунизма чуть не обернулась крахом экономики. Пришлось идти на попятную и возвращаться к рыночным механизмам (к НЭПу).
Однако математические модели, на которые мог бы опираться Госплан, продолжали активно разрабатываться. В частности, были сверстаны первые матрицы межотраслевого баланса – пока еще в очень агрегированном виде – связывающие в единое целое ресурсы, труд и конечный продукт. На основе балансов производилась увязка хозяйственного и государственного управления.
На микроуровне математические методы управления стали применяться в виде линейного программирования, объединявшего методы решения задач, описывавшихся линейными уравнениями, при составлении оптимального по прибыли плана производства; выборе структуры инвестиций; составлении расписаний; разработке маршрутов перевозок. Здесь мы впервые видим математическую поддержку при принятии управленческих решений.
Рассмотрим метод линейного программирования на простом примере.
Предприятие производит две модели – А и В – сборных книжных полок. Их производство ограничено запасами сырья (высококачественных досок) и временем машинной обработки. Для каждого изделия модели А требуется 3 кв.м досок, модели В – 4 кв. м. Предприятие может получить от поставщика до 1700 кв. м досок в неделю.
Для изделия А требуется 12 мин. машинного времени, В – 30 мин. В неделю можно использовать 160 часов машинного времени. Перед менеджментом предприятия стоит вопрос: сколько изделий каждой модели следует выпускать в неделю, если каждое изделие модели А приносит 2 руб. прибыли, а В – 4 руб.?
Очевидно, что даже в такой простой постановке проблемы руководители предприятия не в состоянии сразу определиться с плановыми заданиями. Для выработки оптимального управленческого решения нужен математический расчет.
Обозначим за Х1 – количество выпущенных за неделю полок модели А; за Х2 – количество выпущенных за неделю полок модели В.
Задача состоит в нахождении наилучших значений Х1 и Х2, т.е. таких, которые максимизируют ежедневную прибыль:
Р = 2Х1 + 4 Х2 → max (целевая функция).
Функция принимает экстремальные значения в точках, в которых обращаются в ноль ее производные, либо на границе области определения.
∂Р/∂Х1 = 2; ∂Р/∂Х2 = 4. В нашем случае на при каких Х1 и Х2 производные в ноль не обращаются.
Чтобы увеличивать функцию Р, надо увеличивать Х1 и Х2. Но (и в этом суть проблемы) значения Х1 и Х2 не могут увеличиваться неограниченно. Они ограничены лимитами на сырье и машинное время.
Поскольку Х1 и Х2 выражают еженедельный объем выпускаемых изделий, они неотрицательны: Х1 ≥ 0; Х2 ≥ 0. (1).
Ограничения на наличие досок и машинное время могут быть записаны следующим образом:
3 Х1 + 4 Х2 ≤ 1700 (для досок);
2 Х1 + 5 Х2 ≤ 1600 (для машинного времени). (2).
Следовательно, задача состоит в том, чтобы найти значения Х1 и Х2, удовлетворяющие условиям неотрицательности (1) и ограничениям типа неравенств (2) и максимизирующих функцию Р = 2Х1 + 4 Х2.
Это типичная двухмерная задача линейного программирования. Целевая функция, которая должна быть максимизирована, называется линейной функцией своих переменных. Условия неотрицательности позволяют ограничиться рассмотрением положительного квадранта. Границы его определяются прямыми:
3 Х1 + 4 Х2 = 1700;
2 Х1 + 5 Х2 = 1600.
Решая систему совместно, получаем: Х1 = 300, Х2 = 200. Следовательно, максимальная прибыль составляет:
2 х 300 + 4 х 200 = 1400 руб.
При оптимальном решении оба ограничения превращаются в равенство, что означает полное использование сырья и машинного времени.
В докомпьютерную эпоху использование математических моделей в экономике и управлении было весьма ограниченным. Большие объемы вычислений требовали длительного времени и внушительного штата персонала, осуществляющего счетно-решающие операции. Таким образом, большинство выгод от внедрения математических моделей нивелировалось отсутствием недорогих и достаточно быстродействующих устройств для расчетов.
С появлением транзисторных ЭВМ, а затем и персональных компьютеров, ситуация радикальным образом поменялась. Использование экономико-математических и управленческих моделей стало доступным не только крупным предприятиям и государственным организациям (в первую очередь, военному ведомству, космической отрасли, дешифровальщикам и проч.), но и среднему и малому бизнесу.
В таких сферах, как бухгалтерский и управленческий учёт, автоматизация управления предприятием, взаимодействия с клиентами и поставщиками, стали использоваться экономико-управленческие модели стандартизированного типа, которые при незначительных изменениях адаптируются к потребностям того или иного бизнеса.
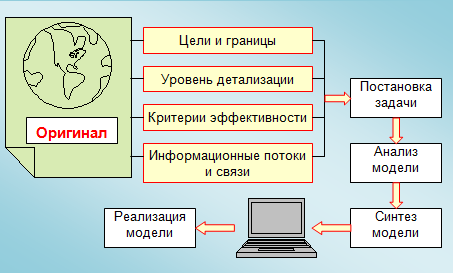
Схематично это можно показать следующим образом. Из совокупности технологических, экономических и управленческих операций выбирается отдельный комплекс работ (оригинал), который подлежит автоматизации (см. рис.2).
Далее определяются параметры модели, уровень детализации, критерии эффективности, информационные потоки и связи. Формализованные задачи переводят на язык математики и алгоритмические вычисления, что дает реализацию модели.
На текущий момент математическая поддержка управленческих решений в бизнесе развита достаточно хорошо. Софтверные компании, специализирующиеся на данном виде предпринимательской деятельности, сейчас создают не только отлично действующие математические продукты, автоматизирующие отдельные участки бизнеса, но и выступают в качестве системных интеграторов, объединяющих отдельные модели в единый комплекс, что дает мощный синергетический и экономический эффект.
Так, с помощью наручных тайм-трекеров некоторые компании предлагают организацию эффективного контроля за персоналом. Управленческая модель позволяет отслеживать в режиме онлайн текущее местонахождение сотрудников, их загрузку, сон или бодрствование (что важно в охранных службах), телефонные звонки, выходы на соответствующие вебсайты. В комплексе с видеомониторингом, системами автоматизированной поддержки заказчик-клиент и различными приложениями обеспечиваются максимальные результаты.
[1] Коммунистическая доктрина предусматривала при построении новых хозяйственных отношений полную отмену денег, так как именно деньги, по мнению большевиков, служат основным инструментом эксплуатации трудящихся. Так, декрет СНК от 2 мая 1919 г. предписывал все платежи между предприятиями и организациями осуществлять не посредством денег, а с помощью бухгалтерских записей. Государство к тому времени уже выплачивало зарплату рабочим и служащим преимущественно продуктами (пайками), – чаще всего той продукцией, которую производило предприятие. Уже была отменена плата за коммунальные услуги, за услуги телеграфа и почты. Лекарства из аптек по рецептам врачей тоже отпускались бесплатно. 19 января 1920 г. «за ненадобностью» был упразднен Народный банк. С 1 января 1921 г. перестал оплачиваться провоз по железным дорогам грузов и почти всех категорий пассажиров. Безденежная экономика быстро привела к разрастанию товарного дефицита и развитию «черного» рынка.
Зарождение менеджмента как науки
Цели и задачи менеджмента. Обеспечение доходности предприятия
Менеджмент как наука и профессия
Специфика менеджмента в России и использование зарубежного опыта
Предприниматели и менеджеры: соотношение интересов и мотивация
Информационные ресурсы в менеджменте
Развитие теории и практики менеджмента в России. Ч.1: А.А. Богданов
Развитие теории и практики менеджмента в России. Ч.2: А.К. Гастев
Развитие теории и практики менеджмента в России. Ч.3: Н.А. Витке
Административная (классическая) школа управления
Школа поведенческих наук (бихевиоризм)