Эффективное распределение ресурсов и оптимальность по Парето. Эффективность и оценочные суждения. Социальный оптимум
Выгоды от конкуренции были, в общем, понятны со времен А.Смита, и, вероятно, даже раньше. Однако точный смысл принципа «совершенная конкуренция эффективно распределяет ресурсы» был формально определен выдающимся итальянским экономистом Вильфредо Парето (1848-1923).
Воспользуемся его определением эффективности, называемой оптимальностью по Парето. Говорят, что ресурсы распределены оптимально по Парето, когда никто не может улучшить положение без того, чтобы в результате для кого-нибудь оно не ухудшилось. В ситуации, оптимальной по Парето, не существует нерационального расходования ресурсов. Оптимальность по Парето предлагает критерий, подсказывающий, имеет ли место в данной конкретной ситуации растрата ресурсов или нет. Но сам по себе этот критерий не говорит нам о том, как следует распределять ресурсы, что справедливо, а что несправедливо.
Проиллюстрируем сказанное графическим примером (см. рис.1).
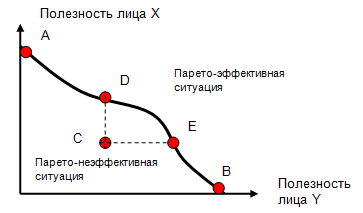
Рис.1. Граница достижимой полезности.
Из графика, представленного на рис.1 видно, что в точке А все ресурсы общества отдаются лицу Х и его полезность максимальна. В точке В максимизируется полезность лица Y. При перемещении из точки А в точку В имеет место компромисс, когда блага передаются от лица Х к лицу Y. Обе точки А и В эффективны по Парето, так как ни в одной, ни в другой ситуации нельзя улучшить положение одной из сторон, не сделав хуже другой. Они, конечно, несправедливы, но оптимальны по Парето.
Рассмотрим далее точки C, D и E. Точка С не является оптимальной по Парето. Двигаясь в направлении вправо вверх, можно улучшать полезность и лица Х и лица Y.
Основное ограничение концепции оптимальности по Парето состоит в том, что она не дает нам никакого способа проранжировать точки на границе достижимой полезности. Здесь должны применяться иные способы.
Эффективность и оценочные суждения. Рынки совершенной конкуренции являются эффективными по Парето в части распределения ресурсов. Другими словами, совершенно конкурентные рынки гарантируют, что экономика автоматически достигнет точки на графике достижимой полезности – точки, в которой ничье положение нельзя улучшить без того, чтобы не ухудшить положение кого-то другого. Но означает ли это, что конкурентные, эффективные по Парето распределения являются в известном смысле социально оптимальными? Совпадает ли экономический оптимум[i] с оптимумом социальным? Ответ будет отрицательным – эти оптимумы чаще всего не совпадают.
Каждый член общества может согласиться, например, с тем, что более равномерное распределение дохода предпочтительнее менее равномерного. Таким образом, такие точки, как точка D на рис.1 в целом предпочтительнее точек, соответствующих крайнему неравенству (точек А и В). Но конкурентной экономике ничто не мешает порождать крайне неравномерное распределение дохода. В этом случае распределение ресурсов было бы оптимальным по Парето, но необязательно социально оптимальным в силу того, что общество предпочло бы находиться в некой другой точке на границе достижимой полезности.
Например, в российском обществе имеется довольно значительная дифференциация населения по доходам и собственности. Политические партии левой ориентации предлагают выравнивать существующее неравенство с точки зрения справедливости, под которой понимается более равномерное распределение дохода. Сделать это предлагается за счет введения прогрессивной шкалы налогообложения, социальных трансфертов и выравнивания ставок заработной платы. За основу предлагается взять скандинавский опыт.
Но тогда, возражают правые партии, порождается уравнительность в экономических отношениях, угасают стимулы к эффективному труду (мы уже рассматривали выше, например, работу М.Фридмена «Свобода, равенство и эгалитаризм», «Капитализм и свобода» и др.). Таким образом, формируется конфликт между социальной справедливостью и экономической эффективностью.
Переводя выявленное противоречие, на язык математической формализации, построим следующую модель. Обозначим за Р1(х) параметр социального развития, а за Р2(х) – экономического. Допустим, что функционирование такой экономико-социальной системы зависит от значений вектора управляемых параметров Х, а значения обоих критериев необходимо максимизировать. Область допустимых значений зададим отрезком Х[a, b] (см. рис.2).
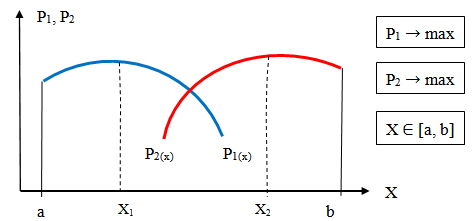
Рис.2. Система конфликтующих критериев Р1 и Р2.
Оптимумы (максимумы) по каждому из критериев достигаются в точках Х1 и Х2 соответственно для Р1(х) и Р2(х). До максимума Х1 и после Х2 критерии Р1(х) и Р2(х) ведут себя согласованно, одновременно увеличиваясь, а затем уменьшаясь. С точки зрения поставленной задачи эти области интереса не представляют (т.е., например, увеличение экономической эффективности вызывает некоторый подъем в социальной жизни и общественных настроениях. И напротив, снижение экономической эффективности ведет к определенному снижению социальных показателей).
Рассматривая теперь область между Х1 и Х2, видим, что увеличение значения критерия Р1(х) (параметра экономического развития) ведет к снижению уровня жизни широких слоев населения и социальным протестам Р2(х), то есть критерии конфликтуют. Этот конфликт отображается в определенную область в пространстве критериев Р1(х) и Р2(х), которая представляет собой совокупность конфликтных решений – множество Парето (см. график на рис.3).
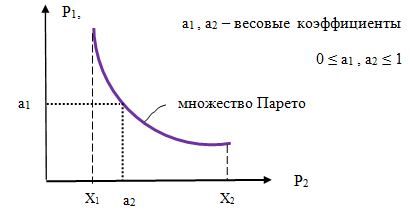
Рис.3. Множество Парето в системе критериев Р1 и Р2.
Взаимосвязь между экономическим и социальным оптимумом может иметь вид обратно пропорциональной зависимости. Выразить количественные соотношения между данными двумя параметрами можно при помощи весовых коэффициентов а1 и а2, придавая им соответствующий «вес» (важность):
Р = а1Р1 + а2Р2, 0 ≤ а1 , а2 ≤ 1.
Проводя, таким образом, линейную свертку критерия, получим некоторый глобальный критерий Р. Выбор соответствующих значений весовых коэффициентов а1 и а2 эквивалентен выбору каких-либо точек на множестве Парето. Количественные оценки весовых коэффициентов могут быть определены экспертами или населением в ходе голосования или опросов.
[i] Экономический (социальный) оптимум − состояние экономической (социальной) системы, наилучшие с позиций ее целей и возможностей в данных условиях









