Важной составной частью экономико-математического моделирования, имеющей обширное практическое применение, является теория массового обслуживания.[1] Название теории довольно точно отражает её сущность, – теория массового обслуживания вбирает в себя комплекс теоретических вопросов оптимального построения и эксплуатации систем массового обслуживания. То речь идет о таких системах, которые часто встречаются в технике и экономике и предназначены для многократного использования при выполнении однотипных задач.
Теория массового обслуживания оформилась в середине ХХ в.; ее основоположником считается известный датский ученый А.К. Эрланг, который решил ряд задач по теории массового обслуживания с отказами.
Во многих областях экономики спорта активно используются системы специального назначения, реализующие выполнение типовых задач с циклическим повторением операций. Такие системы получили название систем массового обслуживания. В качестве примеров систем массового обслуживания можно рассматривать спортивные сооружения (стадионы, спорткомплексы, ледовые арены и прочее), спортивные организации всех организационно-правовых форм (единоличные владения, партнёрства, акционерные общества всех типов), билетные кассы, предприятия торговли и многие другие объекты.
Термин «система» означает совокупность частей, связанных общей функцией, то есть некоторую целостную структуру взаимодействующих элементов. Не являются исключением в этом смысле и системы массового обслуживания, которые включают в себя некоторое число обслуживающих устройств, которые называются каналами или линиями обслуживания. Роль каналов обслуживания могут выполнять различные устройства, линии связи, приборы или люди, производящие те или иные операции, — например, транспортные пути, кассиры или операторы.
Системы массового обслуживания различаются по своему построению и уровню сложности. Их принято подразделять на одноканальные и многоканальные.
Как правило, в экономико-математическом моделировании систем массового обслуживания и других объектов элементы моделирования обозначают прямоугольником, у которого имеется вход и выход, обозначаемые стрелками (см. рис.11.2). Если модель адекватна оригиналу, то изменение сигнала на входе и выходе у них должно быть одинаковым. При этом внутренняя структура моделируемого объекта и процессы, протекающие в нем, в модели не показываются, то есть модель представляет собой так называемый «чёрный ящик».
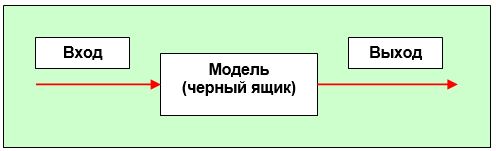
Рис.11.2. Схематическое изображение одноканальной модели.
Все системы массового обслуживания предназначены для обработки некоторого потока заявок [2], поступающих случайным образом на вход системы. Обслуживание поступивших заявок может производиться системой за разные временные интервалы, так как время обработки заявок зависит от многих случайных величин. Пока заявка обрабатывается, канал считается занятым. По окончании обслуживания заявки канал освобождается и находится в состоянии ожидания поступления новой заявки.
Очевидно, что случайный характер поступления заявок и времени их обслуживания создаёт для систем массового обслуживания режим работы с неравномерной нагрузкой, – в отдельные периоды интенсивность потока заявок заставляет работать систему с перегрузкой, в другие, в отсутствие заявок, система простаивает. Причем, даже функционируя в режиме максимальной загрузки, система массового обслуживания допускает создание очереди, которую часть заявок покидает, если ожидание затягивается. В таких случаях возникает необходимость введения в систему дополнительных линий обслуживания. Такая система массового обслуживания становится многоканальной (см. рис.11.3).
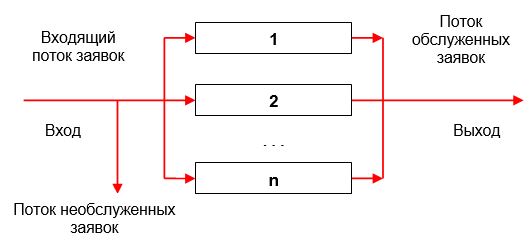
Рис.11.3. Многоканальная система массового обслуживания
Как следует из рисунка 11.3, каждая система массового обслуживания содержит следующие элементы:
- Каналы обслуживания;
- Входной поток заявок;
- Очередь;
- Выходящий поток обслуженных заявок.
В спортивной индустрии и других отраслях экономики используется большое количество систем массового обслуживания, каждая из которых содержит различное число каналов обслуживания, имеет свою производительность и организационную структуру. В зависимости от указанных характеристик система массового обслуживания обладает определённой эффективностью функционирования (пропускной способностью). Если какая-либо система массового обслуживания со временем перестаёт справляться со своими задачами, её заменяют на более эффективную, которая более полно удовлетворяет увеличившимся объемам заявок.
В качестве иллюстрации прикладного применения теории массового обслуживания приведем простую задачу.
Задача
Стадион небольшого города обслуживает касса с одним окном. В дни проведения соревнований численность покупателей билетов возрастает и интенсивность покупок составляет 0,45 чел./мин. Кассир затрачивает на обслуживание болельщика в среднем 2 минуты. Определить среднее число покупателей у кассы и среднее время, затрачиваемое болельщиком на приобретение билета.
Решение:
Данная процедура обслуживания моделируется одноканальной системой массового обслуживания с ожиданием без ограничений на длину очереди и на время ожидания. Параметры системы:
- Число каналов n = 1;
- Интенсивность входного потока λ = 0,45 чел./мин.
- Среднее время обслуживания одной заявки Тоб. = 2 мин.
Следовательно, интенсивность потока обслуживания μ будет составлять: μ = 1/ Тоб. = 0,5 (чел./мин.), а нагрузка системы ρ определится как ρ= λ/μ = 0,45/0,5 = 0,9 (эрланга).
Среднее число покупателей у кассы определится как
N сис. = ρ/(1 – ρ) = 0,9/(1 – 0,9) = 9 (чел.).
Среднее время, которое болельщик затрачивает на приобретение билета, складывается из среднего времени пребывания в очереди. Его можно подсчитать по формуле:
Тсис. = 1/(1 – ρ) = 1/0,5(1 – 0,9) = 20 (мин.).
Таким образом, получаем следующий результат: очередь у кассы в среднем составляет 9 человек, а время затрачиваемое болельщиком на приобретение входного билета на стадион – 20 минут. Очевидно, что такой результат не является удовлетворительным и в «пиковые» периоды администрации стадиона следует подключать к продаже билетов ещё одного кассира.
————————————————
[1] Заявками в теории массового обслуживания называются чередующиеся события, которые наступают в заранее неизвестные промежутки времени.
[2] За рубежом теорию массового обслуживания называют также теорией очередей или теорией линий ожидания. Термин «теория массового обслуживания» предложил российский ученый А.Я. Хинчин.









