В современной экономике спорта довольно широко используется математический аппарат, – анализируются графики и ряды различных зависимостей, выводятся аналитические формулы, проводится математическая обработка статистических данных, производится компьютерное моделирование экономических процессов. В проектировании спортсооружений также широко используются системы автоматического проектирования и симуляции. Более того, в России уже официально зарегистрирован и новый вид спорта, основанный на математике и информационно-компьютерных технологиях — киберспорт, который стремительно набирает популярность во всём мире.
Чем же вызвано такое активное проникновение математики в экономику? С какой целью внедряются в спортивный бизнес вычислительные алгоритмы? Ответить на этот вопрос можно следующим образом. Центральной проблемой экономики является проблема рационального выбора. Чтобы делать правильный и обоснованный выбор (или осуществлять прогноз) необходима математическая поддержка процесса принятия решений. Поэтому роль математических методов в экономике непрерывно возрастает. Кроме того, математическое моделирование полезно для более полного понимания сущности происходящих процессов, уяснения их экономической природы и движущих сил. В связи с тем, что в настоящее время многие математические теории и их прикладные направления хорошо разработаны (такие, как линейная алгебра, математический анализ, теория вероятностей, корреляционный и дисперсионный анализ, методы скалярной и векторной оптимизации), то пользователям можно задействовать возможности мощного и развитого математического аппарата.
К сказанному следует добавить, что виртуальное компьютерное моделирование и использование математического аппарата подчас существенно снижает издержки организаций и компаний при осуществлении планирования и прогнозирования экономических мероприятий. Экономия средств в данном случае образуется за счёт внедрения модельных экспериментов и оптимизационных методов решения многих видов задач.
Остановимся несколько подробнее на понятии моделирования и модельного эксперимента. Общеизвестно, что в основе изучения экономических и иных систем всегда лежит эксперимент – реальный или модельный.[1] Смысл реального эксперимента – это изучение свойств на самом практически действующем объекте. Например, возьмём реально существующий и действующий объект – спортивное сооружение в виде зимнего Дворца спорта (или многофункционального объекта, легко трансформируемого в концертный зал, теннисный корт или иную площадку). Для того чтобы выяснить оптимальную цену билетов на игры чемпионата страны по хоккею, можно провести ряд экспериментов по наполняемости зрительской аудитории при различных ценах билетов. Однако такое экспериментирование приводит к неизбежным потерям части прибыли Дворцом спорта, что является крайне нежелательным. В таких случаях целесообразно проводить модельный эксперимент, то есть такой, который проводится не на реально действующем объекте, а на его виртуальном аналоге – модели. Построение моделей и изучение свойств систем при помощи таких моделей называется моделированием.
Моделирование оказывается незаменимым инструментом и при построении экономических прогнозов, то есть вероятных суждений о состоянии какого-либо явления или системы в будущем. Прогнозирование является одной из форм предвидения перспектив развития событий, которое в экономике является ценнейшим ресурсом, так как предвидение – залог будущей прибыли.
При изучении экономических систем и прогнозировании их будущего состояния чаще всего используют математическое моделирование (так как эксперимент на реальном объекте, как было сказано выше, ведет к необоснованным издержкам). Под математическим моделированием понимается концентрация наших знаний, представлений и гипотез об оригинале, записанную с помощью математических соотношений.
Математическая модель представляет собой упрощённую модель оригинала. В результате такого упрощения происходит сокращение размерности состояний исходной системы. В то же время сформированная модель должна вести себя также как и оригинал, то есть между оригиналом и математической моделью должно быть взаимное соответствие.
Построение экономико-математических моделей включает в себя несколько этапов (см. рис.11.1).
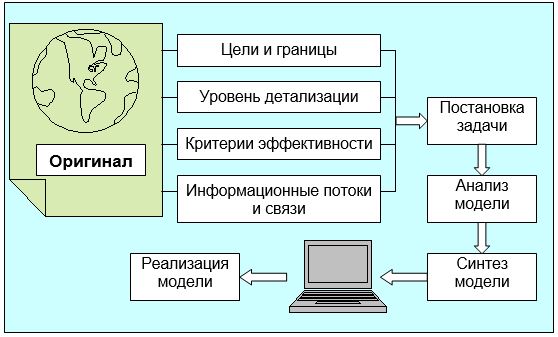
Рис.11.1. Процесс построения моделей.
Формирование экономико-математической модели начинается с постановки задачи, которая, в свою очередь, открывается определением целей моделирования. Далее, исходя из целей исследования, устанавливаются границы изучаемой системы, условий её функционирования и необходимый уровень детализации моделируемых процессов. Кроме того, в постановку задачи включаются критерии оценки эффективности функционирования оригинала и возможные ограничения на их значения. Большую роль играет также описание потоков информации, циркулирующих между оригиналом и внешней средой, взаимосвязь внутренних элементов, описание ограничений на выделенные ресурсы.
Следующим этапом построения модели является синтез, то есть формирование структуры и описание параметров модели. Структурный синтез заключается в построении в рамках поставленной задачи некоторого количества альтернативных вариантов моделей, отличающихся степенью детализации и учёта тех или иных особенностей функционирования оригинала.
Этап анализа модели заключается в изучении её свойств и поведения в различных условиях функционирования. На этой стадии производится выбор и расчёт критериев эффективности для каждой из построенных на этапе синтеза моделей. Такими критериями могут быть, например, минимум издержек на единицу производимой продукции или максимум качества предоставляемых потребителям товаров и услуг.
Различают следующие виды математических моделей:
- Аналитические – это модели, представляющие собой совокупность аналитических выражений и зависимостей;
- Имитационные – это модели, основанные на компьютерном эксперименте; являются переложением на машинный язык описаний моделируемых объектов. Эти модели позволяют имитировать функционирование систем на компьютере, производить при этом измерения и обработку необходимых данных;
- Численные – это модели, представленные в виде различных численных методов и схем, как правило, обеспечивающих приближённое решение задачи;
- Алгоритмические – это модели, представленные алгоритмами в виде опредёленной логической последовательности выполнения операций на компьютере.
Следует отметить, что в теории и практике экономико-математического моделирования используется и ряд других типов моделей, характеризующихся разной степенью сложности и различным предназначением.
————————————————————
1 Проверка практикой также является своего рода реальным экспериментом.









